COMPREHENSIVE ACCESSIBILITY OF EQUATIONS BY VISUALLY IMPAIRED

Akashdeep Bansal, Indian Institute of Technology Delhi, New Delhi, India, akashdeep@cse.iitd.ac.in
M. Balakrishnan, Indian Institute of Technology Delhi, New Delhi, India, mbala@cse.iitd.ac.in
Volker Sorge, University of Birmingham, United Kingdom, v.sorge@cs.bham.ac.uk

Abstract

Persons with visual impairments can access digital information through screen reading software. Still, accessing mathematical equations is challenging due to their non-linearity. We propose to improve the accessibility of equations by associating a cognitive complexity metric with each equation and then to use this metric to modify their audio rendering. For example, this will allow audio rendering of complex equations by substituting chunks with variables. This will potentially reduce the cognitive load in comprehending equations by persons with visual impairments. Further, this metric needs to be personalized on the basis of various user characteristics.

Introduction

Screen reading software is primarily designed to provide access to linear content such as text, to persons with visual impairment. But rendering mathematical equations is still challenging. However, access to equations is absolutely essential in the domain of STEM education. Mathematical equations are non-linear in nature due to the use of 2-D mathematical constructs such as superscript, subscript, fraction, square-root, parenthesis, etc. However, audio is linear, which makes it hard to render equations without ambiguity, verbosity, and cognitive load. To understand this, let us take an example:

Try to imagine how screen reader will read out this equation. Similarly, how complicated it will be for a person with dyslexia to comprehend the same.

Various cues have been proposed to remove ambiguity due to non-linearity, when audio rendering the mathematical equations. Some of them also try to optimize for cognitive load, verbosity, and naturalness. The proposed cues include lexical [4], prosodic [13], earcons [15], spearcons [1], audio spatialization [12], and auditory [11], etc. In various user studies [12,15,5,7,11] it has been found that none of the cues was able to make rendering completely unambiguous, natural, succinct, and cognitively efficient.

As the complexity of the equation increases, rendering with proposed cues becomes more and more ineffective. Summary [8], Variable substitution [13], and hierarchical navigation [5] are some of the alternatives that have been proposed in the literature for handling complex equations. Still, it is not clear how to quantify the complexity.

In this dissertation, we are focusing on answering the following questions:

1. What are the characteristics of an equation, which can quantitatively analyze the cognitive complexity of an equation in an auditory interface?
2. How much is the weightage of each characteristic towards the total complexity?
3. How these weights will vary on the basis of user characteristics (such as IQ, listening ability, age, educational background, familiarity with the content, cues choice, etc.)?
4. What can be a cognitively efficient delivery mechanism for complex equations?
5. How the semantic disambiguation of an equation can be done on the basis of the context?
6. What will be the effect of semantics on the complexity metric and delivery mechanism?

Cognitively efficient abstraction of complex equations

MathJax [2,3] and AsTeR [13] are some of the tools which provide audio rendering of equations as well as abstraction for better comprehension. MathJax abstracts out on the basis of rendered elements' size. Whereas, in AsTeR, Raman proposes abstraction on the basis of subtree's weight, considering all nodes have equal weight. Even, some of the commonly used computing systems such as Mathematica [10], and Maple [9], etc. also abstract out very long equations for proper display on the screen. In spite of availability of abstraction among various tools and significant time that has elapsed, there has been no validation of their effectiveness as yet. We plan to approach this by answering the following two questions -

1. Given an equation, how can we determine whether it is cognitively complex for a user or not?
2. Given a complex equation, how should the variable substitution take place so that the resultant equation as well as the substituted chunks are not complex?

To answer these questions, we are conducting a series of user studies. The data from these user studies will enable us to find the relation between the tree complexity and the cognitive complexity of an equation. This will also be utilized for finding a common threshold to classify equations into categories: cognitively simple and complex. Further, validation of the threshold, cognitive complexity metric, and effectiveness of variable substitution will be done in another set of user studies.

Let us try to understand this with an example using two equations from our test bench. These equations don't have any context associated, physical interpretation, and pattern in variables and operators. This is done to eliminate the bias, which might affect the comprehension of the equations. Consider that Eq. 1's cognitive complexity comes out to be near threshold. Whereas, Eq. 2's comes out to be much higher than the threshold.

Then, maybe we can render the Eq. 2 as

where, 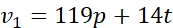, , 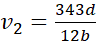and

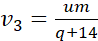
Further, experience can be enhanced by providing random access of substituted variables' values.

User Study

We are planning to conduct three user studies. The objectives of the user studies are as follows --

1. To find the relationship between the tree complexity and the cognitive complexity of an equation. Also, to find out the common threshold across all the participants for classifying equations as cognitively complex or simple.
2. To validate the findings of the first user study.
3. To evaluate the usefulness of the variable substitution for cognitively effective audio rendering of complex equations.

Participants

We are conducting user studies with approximately twenty five persons with visual impairments having STEM background. Their age varies from twelve to forty years. Some of them are congenitally blind and some are late blind or still have some sight.

Equation Test Bench

Self-constructed algebraic equations having no patterns among operators and variables were used. It was also taken care that selected equations should not have any familiarity to the user in terms of context or physical interpretation, to eliminate its bias. Eq. 1 and Eq. 2 are examples of equations in the test bench.

Study Setup

User Study 1: Find Relationship between tree and cognitive complexity, and common threshold

Thirty equations of varied tree complexities were chosen from the test bench. They were divided into nine sets of ten equations each. We made sure that every equation appeared in exactly three sets and that the variation in tree complexity was uniform across the sets. Nine users participated in this study and one set was presented to a user through MathPlayer [14,5] using ClearSpeak [6] rules. Users were expected to reproduce the equation after every utterance. Maximum of five utterances were allowed in case of lack of confidence or error in the reproduction.

Now, we are analyzing the data for finding the relation between the tree and cognitive complexity (in terms of time taken, number of attempts and mistakes, etc.) of an equation, and the common threshold.

User Study 2: Validate complexity relation and threshold

The setup of this study is similar to the previous study except that the set of equations is different and the set of users is a mix of new and users from previous study.

User Study 3: To evaluate the effectiveness of variable substitution for cognitively complex equations

On the basis of the findings in previous studies, a new set of cognitively complex equations with varied complexity will be created. Variable substitution will be performed keeping in mind that the resultant equation's cognitive complexity as well as the substituted chunk's cognitive complexity should not exceed the threshold value. Here, we are planning to use MathJax, as it allows collapsing on the basis of the threshold. The threshold will be computed based on the derived complexity metric. Effectiveness of the approach will be tested by analyzing the various factors including number of iterations taken to comprehend the equation, average time taken, and user rating, etc.

Conclusion

The objective of this research is to improve the user experience and comprehension of complex equations. The proposed approach will evolve a metric for representing complexity of equations and their efficient rendering. Further, this metric will be optimized on the basis of context as well as user characteristics. Further, the scope of this work can be extended to generate personalized verbal description of diagrams and enhancing readability of equations in Braille interface.

Acknowledgments

This work is supported under projects funded by Ministry of Human Resource Development, Govt. of India under the IMPRINT and SPARC scheme.

References

1. Enda Bates and Dónal Fitzpatrick. 2010. Spoken mathematics using prosody, earcons and spearcons. In International Conference on Computers for Handicapped Persons. Springer, 407–414.
2. Davide Cervone, Peter Krautzberger, and Volker Sorge. 2016a. New accessibility features in MathJax. In 31th Annual International Technology and Persons with Disabilities Conference Scientific/Research Proceedings. California State University, Northridge.
3. Davide Cervone, Peter Krautzberger, and Volker Sorge. 2016b. Towards universal rendering in MathJax. In Proceedings of the 13th Web for All Conference. ACM, 4.
4. Larry A Chang, Carol M White, and Lila Abrahamson. 1983. Handbook for spoken mathematics. Livermore, CA: Lawrence Livermore National Laboratory.
5. Lois Frankel, Beth Brownstein, and Neil Soiffer. 2014. Navigable, customizable TTS for Algebra. In 28th Annual International Technology and Persons with Disabilities Conference Scientific/Research Proceedings. California State University, Northridge.
6. Lois Frankel, Beth Brownstein, Neil Soiffer, and Eric Hansen. 2016. Development and initial evaluation of the ClearSpeak style for automated speaking of algebra. ETS Research Report Series 2016, 2 (2016), 1–43.
7. Ed Gellenbeck and Andreas Stefik. 2009. Evaluating prosodic cues as a means to disambiguate algebraic expressions: an empirical study. In Proceedings of the 11th international ACM SIGACCESS conference on Computers and accessibility. ACM, 139–146.
8. Douglas J Gillan, Paula Barraza, Arthur I Karshmer, and Skye Pazuchanics. 2004. Cognitive analysis of equation reading: Application to the development of the math genie. In International Conference on Computers for Handicapped Persons. Springer, 630–637.
9. Maplesoft Maple. 2016. a division of Waterloo Maple Inc. Waterloo, Ontario (2016).
10. Wolfram Mathematica. 2009. Wolfram research. Inc., Champaign, Illinois (2009).
11. Emma Murphy, Enda Bates, and Dónal Fitzpatrick. 2010. Designing auditory cues to enhance spoken mathematics for visually impaired users. In Proceedings of the 12th international ACM SIGACCESS conference on Computers and accessibility. ACM, 75–82.
12. Venkatesh Potluri, SaiKrishna Rallabandi, Priyanka Srivastava, and Kishore Prahallad. 2014. Significance of Paralinguistic Cues in the Synthesis of Mathematical Equations. In Proceedings of the 11th International Conference on Natural Language Processing. 395–402.
13. TV Raman. 1994. Audio system for technical readings. Technical Report. Cornell University.
14. Neil Soiffer. 2007. MathPlayer v2.1: web-based math accessibility. In Proceedings of the 9th international ACM SIGACCESS conference on Computers and accessibility. ACM, 257–258.
15. Robert D Stevens, Alistair DN Edwards, and Philip A Harling. 1997. Access to mathematics for visually disabled students through multimodal interaction. Human-computer interaction 12, 1 (1997), 47–92.

About the Authors